
изм. от 12.10.2013 г - ( )
ПРЕДИСЛОВИЕ
Концепция времени является одной из наименее известных человечеству, по крайней мере, современному. Огромный прорыв в понимании природы времени совершили Дьюи Ларсон и Николай Козырев. В то же время, можно сказать, что со свойствами времени работало большинство альтернативных ученых, независимо от того понимали они это или нет. В 1959 году Д. Ларсон опубликовал свою книгу “Структура физической вселенной». Он считал, что и пространство и время - это просто аспекты обратного отношения, называемое движением. Он часто приводил аналогию с коробкой, где снаружи коробки находится пространство, а внутри коробки – время, сама же коробка является движением. То есть вы имеете дело с пространством (снаружи), временем (внутри) и движением (коробка). Эти три концепции всегда взаимосвязаны и не могут работать независимо друг от друга. Со временем теория Ларсона стала известна как «Физическая теория обратной взаимообусловленности пространства и времени». Поэтому введение понятия трехмерного времени дало возможность связать воедино многие фрагменты.
Как только мы осознаем, что существуем одновременно в двух разных сферах - пространственной, материальной для тела, и временной, космической для души, легко понимаются все экстрасенсорные способности.
А вернувшись в класс математики средней школы и вспомнив одну довольно раздражающую в то время концепцию, известную как мнимое число, начинаешь понимать, что оно не настолько уж и мнимо. Число, которое действует подобно вращению и не существует нигде в пространстве как количество. С точки зрения школьника, с мнимыми числами труднее иметь дело, чем с дробями! Кстати, сейчас в школах даже не дают понятия комплексных чисел.
С нашей перспективы, время - это полярная сфера, естественно совершающееся вращение. Материальный и космический секторы лучше всего описываются как сложные соединения друг с другом, поэтому пространство реально, а время мнимо, не в смысле “веры”, а в смысле мнимого числа. Поймите комплексное число - комбинацию реального и мнимого чисел, и вы поймете связь между пространством и временем, ян и инь, телом и душой.
Поскольку координатное время не является мнимым, забавные маленькие мнимые числа на самом деле демонстрируют взаимодействие между физическим и метафизическим,… по одной ноге в обеих реальностях. Это открывает дверь к тому, что пребывает за пределами пространства и времени.
А теперь, имея ввиду вышеизложенное, взгляните на комплексные числа несколько более объемно, и вы увидите в плоских формулах математики многомерность.
КОМПЛЕКСНЫЕ ЧИСЛА
В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ
Если решить уравнение x2 + 2х + 5 = 0 с использованием формулы корней квадратного уравнения, мы получим
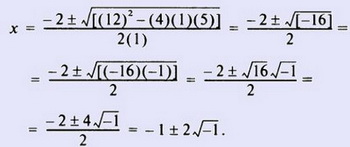
В действительных числах определить значение √-1 невозможно.
Однако если задать оператор j формулой j = √-1, то можно найти решение этого уравнения в виде х = - 1 ± j2.
-1 + j2 и -1 - j2 известны как комплексные числа. Оба решения имеют вид а + jb, где а - действительная часть, a jb - мнимая часть. Число вида а + jb называется комплексным числом в декартовой системе координат.
Поскольку
j = √-1, то j2 = -1,
j3 = j2x j = (-1) х j = -j,
j4 = j2 х j2 = (-1) х (-1) = 1
и
j23 = j x j22 = j x (j2)11 = j x (-1)1 = j x (-1) = -j.
В чистой математике для обозначения √-1 используется символ i (это первая буква английского слова imaginary - мнимый). Однако i - это также обозначение электрического тока в инженерных науках, и во избежание путаницы для представления √-1 используется следующая буква алфавита, j.
Пример: Квадратное уравнение 2x2 + 3х + 5 = 0 решается следующим образом:
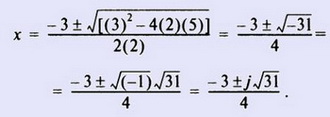
Следовательно 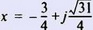 , или -0,75 ±j1,392, с точностью до трех знаков после запятой. , или -0,75 ±j1,392, с точностью до трех знаков после запятой.
Отметим, что график y = x2 + 2х + 5 = 0 не пересекает ось х, следовательно, уравнение x2 + 2х + 5 = 0 не имеет действительных корней.
КОМПЛЕКСНАЯ ПЛОСКОСТЬ
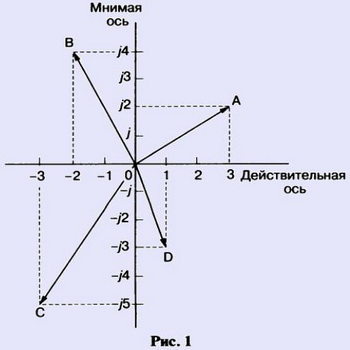
Комплексное число можно графически представить в прямоугольной системе координат. Горизонтальная ось (ось х) используется для представления действительной части, а вертикальная (ось у) - для представления мнимой части. Таким образом, любое комплексное число можно отобразить в виде точки комплексной плоскости. На рис. 1 точка А представляет комплексное число (3 + j2) и имеет координаты (3, j2) на графике. На
рис. 1 также показаны точки В, С и D, представляющие комплексные числа (-2 + о4), (-3 - j5) и (1 - j3) соответственно.
 СЛОЖЕНИЕ И ВЫЧИТАНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
СЛОЖЕНИЕ И ВЫЧИТАНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Два комплексных числа складываются/вычитаются посредством раздельного сложения/вычитания двух их действительных и двух мнимых частей.
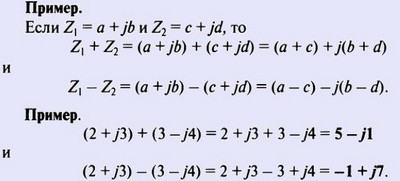
УМНОЖЕНИЕ И ДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Чтобы перемножить комплексные числа, необходимо перемножить все величины в мнимой и действительной частях, как будто они действительные, а затем упростить, используя выражение j2 = -1..
Следовательно,
(а + jb)(c + jd) = ас + a(jd) + (jb)c + (jb)(jd) = ас + jad + jbe + j2bd = (ac - bd) + j(ad + be), поскольку j2 = -1.
Пример.
(3 + j2)(4 - j5) = 12 - j15 +j8 - j210 = (12 - (- 10)) +j(-15 + 8) = 22 - j7.
Комплексно-сопряженное для комплексного числа получают,
изменив знак перед мнимой частью. Следовательно, комплексно-сопряженное для (а + jb) - это (а - jb). Произведение двух комплексно-сопряженных всегда равно действительному числу.
Например: (3 + j4)(3 - j4) = 9 - j12 + j12 - j216 = 9 + 16 = 25.
Значение (а + jb)(a - jb) «на глаз» можно оценить как а2 + b2.
Деление комплексных чисел осуществляют, умножая числитель и знаменатель на комплексно-сопряженное к знаменателю.
Пример.
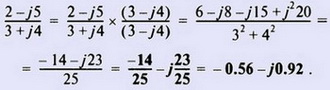 КОМПЛЕКСНЫЕ УРАВНЕНИЯ
КОМПЛЕКСНЫЕ УРАВНЕНИЯ
Если два комплексных числа равны, то их действительные части равны и их мнимые части равны. Следовательно, если a +jb = с +jd, то а = с и b = d.
Пример. Решить комплексное уравнение (1 + j2)(-2 - jЗ) = а + jb.
(1+ j2)(-2 - j’З) = a + jb,
-2 - jЗ - j4 - j26 = а + jb.
Следовательно, 4 - j7 = а + jb.
Приравнивая действительную и мнимую части, получаем а = 4 и b = -7.
ПОЛЯРНАЯ ФОРМА ЗАПИСИ КОМПЛЕКСНЫХ ЧИСЕЛ
Пусть комплексное число Z равно х + jy, как показано на рис. 2. Пусть расстояние OZ равно г, и угол, который OZ составляет с положительным направлением действительной оси, равен Θ.
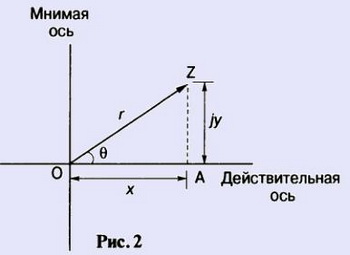
Из определения тригонометрических функций: х = г cos Θ и у = г sin Θ.
Z = r(cos Θ + sin Θ) обычно сокращают до r Θ, это полярная
форма записи комплексного числа. Θ, это полярная
форма записи комплексного числа.
г называется модулем Z и записывается как mod Z или IZI.
г определяют по теореме Пифагора из треугольника OAZ с рис.2, т. е.
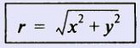
Θ называется аргументом Z и записывается как arg Z.
Из треугольника ОАZ находим arg Z = Θ = arctg y/x
При переходе от декартовой формы записи к полярной или наоборот очень важно построить диаграмму, чтобы определить, какому квадранту принадлежит комплексное число.
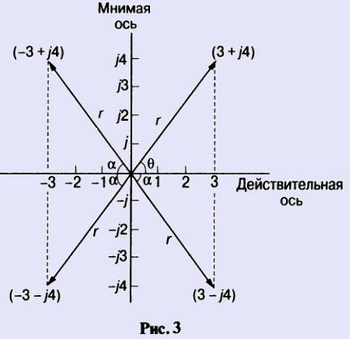
Пример. Выразить: а) 3 +j4 и б) -3 + j4 в полярной форме.
а) Число 3 + j4 показано на рис. 3, оно лежит в первом квадранте.
Модуль г = √(32 + 42) = 5 ,ааргумент Θ = arctg 4/3 = 53,13o = 53°8'.
Следовательно, 3 + j4 = 5 53,13o. 53,13o.
б) Число -3 + j4 лежит во втором квадранте.
Модуль г = 5, угол α = 53,13o из вычислений в п. а).
Аргумент Θ = 180o - 53,13o = 126,87o (т. е. аргумент нужно измерять относительно положительного направления действительной оси).
Следовательно, -3 + j4 - 5 126,87o . 126,87o .
Аналогично можно показать, что (-3 - j4) = 5 233,13o или
5 233,13o или
5 -126,87o (принято использовать главное значение, т. е. численно наименьшее, чтобы выполнялось условие -π < Θ < π) и
(3 - j4) = 5 -126,87o (принято использовать главное значение, т. е. численно наименьшее, чтобы выполнялось условие -π < Θ < π) и
(3 - j4) = 5 -53,13o. -53,13o.
 ПРИМЕНЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
ПРИМЕНЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Существует несколько применений комплексных чисел в науке и технике, в частности в теории переменного тока, при векторном анализе в механике, в аэро- и гидродинамике. Бернулли применил комплексные числа для вычисления интегралов. Их широко использовал и отец русской авиации Н. Е. Жуковский при разработке теории крыла, автором которой он является.
Результат умножения фазового вектора на j - его поворот в положительном направлении (т. е. против часовой стрелки) в комплексной плоскости на 90o без изменения его длины. Аналогично при умножении фазового вектора на -j он поворачивается на -90o. Эти свойства используются в теории переменного
тока, поскольку некоторые величины на фазовых диаграммах лежат под углом 90o друг к другу. Например, в последовательном RL-контуре, показанном на рис. 5а, VL опережает I на 90o (т. е. I запаздывает относительно VL на 90o) и может быть записан как jVL, вертикальная ось считается мнимой осью комплексной плоскости. Таким образом, VR + jVL = V, и поскольку VR = IR, V= IXL (где XL - индуктивное сопротивление, 2πfL Ом), а V = IZ (где Z - полное сопротивление), то R + jXL = Z.
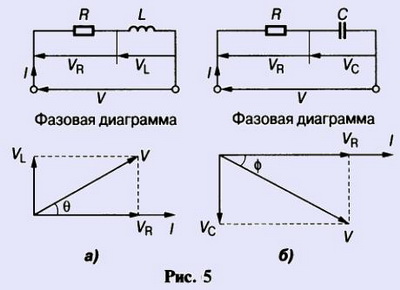
Например, Z = (4 + j7) Ом представляет полное сопротивление, состоящее из последовательно соединенных омического сопротивления величиной 4 Ом и катушки индуктивности с индуктивным сопротивлением 7 Ом. Аналогично для RC-контура, показанного на рис. 5б, Vс запаздывает на 90o относительно I (т. е. I опережает Vс на 90o), и VR - jVc = V, откуда R - jXc = Z (где Хс - емкостное сопротивление величиной 1/2πfL Ом).
Например, Z= (5 - jЗ) Ом представляет полное сопротивление, состоящее из последовательно соединенных омического сопротивления величиной 5 Ом и емкостного сопротивления.
величиной 3 Ом.
Данный пример очень хорошо помогает представить откуда берется, например, "дополнительное пространство", необходимое для параллельных Вселенных, так упорно "вычисляемое" даже современной математикой. Я уже не говорю о х'Арийской арифметике, учитывающей многомерность, как само собой разумеющееся. Если хотите, можно назвать индуктивное и емкостное сопротивления - "величинами сопротивления времени", а емкость конденсатора - "количеством свободного времени", которое можно заполнить электричеством. Но тогда нам придется задать себе вопрос: - А что же такое электричество?
Как написал Н.А. Козырев еще в 1971 году: «...при малой плотности время с трудом воздействует на материальные системы. Возможно, что наше психологическое ощущение пустого или содержательного времени имеет не только субъективную природу, но имеет и объективную физическую основу».
"...время благодаря своим активным свойствам может вносить в наш мир организующее начало и тем противодействовать обычному ходу процессов, ведущему к разрушению и производству энтропии. Это влияние времени очень мало в сравнении с обычным разрушающим ходом процессов, однако оно в природе рассеяно всюду, и потому имеется возможность его накопления. Такая возможность осуществляется в живых организмах и массивных космических телах, в первую очередь в звездах. Для Вселенной в целом влияние активных свойств времени проявляется в противодействии наступлению ее тепловой смерти."
Хотел написать о мнимых числах, а получилось о реальном времени...
|

