 ГЕОМЕТРИЯ ПЛАТОНОВЫХ ТЕЛ
ГЕОМЕТРИЯ ПЛАТОНОВЫХ ТЕЛ
изм. от 24.06.2013 г - (дополнено)
К основным пяти Платоновым телам относятся: октаэдр, звездный тетраэдр, куб, додекаэдр, икосаэдр.
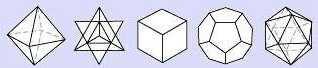
Каждый из геометрических паттернов, будь то атомное ядро, микрокластеры, глобальная решетка или расстояния между планетами, звездами, галактиками, является одним из пяти основных “Платоновых Твердых Тел”.

Почему подобные паттерны так часто возникают в природе? Один из первых намеков: математики знали, что эти формы обладают большей “симметрией”, чем любая трехмерная геометрия, которую мы можем создавать.
Из книги Роберта Лолора "Сакральная геометрия" мы можем узнать, что индусы сводили геометрии Платоновых Тел в структуру октавы, которую мы видим для звука и света (ноты и цвета). Греческий математик и философ Пифагор, посредством процесса последовательного деления частоты на пять, впервые разработал восемь “чистых” тонов октавы, известных как диатоническая шкала. Он взял однострунный “монохорд”, и измерил точные длины волны при проигрывании разных нот. Пифагор показал, что частоту (или скорость вибрации) каждой ноты можно представить в виде отношения между двумя частями струны, или двумя числами, отсюда и термин “диатонические отношения”.
Нижеприведенная таблица перечисляет геометрию в определенном порядке, увязав ее с числом спирали фи (спираль Фибоначчи). Это дает полную и законченную картину, как работают вместе различные вибрации. Она основана на присвоении ребрам куба длины, равной “1”. Затем мы сравниваем с этой величиной ребра всех других форм, больше они или меньше. Мы знаем, что в Платоновых Телах каждая грань имеет одинаковую форму, каждый угол идентичен, каждый узел находится на одинаковом расстоянии от всех других узлов, и каждая линия имеет одинаковую длину.
1 Сфера (нет граней)
2 Центральный икосаэдр 1/фи2
3 Октаэдр 1/√2
4 Звездный тетраэдр √2
5 Куб 1
6 Додекаэдр 1/фи
7 Икосаэдр фи
8 Сфера (нет граней)
Это поможет понять, как при помощи вибраций спирали фи платоновы тела постепенно перетекают одно в другое.
В ведической космологии содержится четко объясненное расположение сферы и всех пяти Платоновых Тел в Октаве. В этой системе сфера и икосаэдр наблюдаются дважды, именно так мы получаем октаву, состоящую из семи позиций: шести основных форм – пяти Платоновых Тел и сферы.

Ричард Томпсон и другие раскрывают, что древняя ведическая культура Индии обладала высокой степенью научного продвижения, включая знание Солнечной Системы, летательного аппарата и ядерного оружия. Усматривается явная связь с эфирной/”пространственной” космологией.
Создавая основанные на октаве “модулярные функции”, индус Шриниваса Рамануйян обладал знанием ведической космологии. Его система и по сей день остается основной математической системой “более высоких измерений”, используемой в теории суперструн.
Экзотические числовые операции Рамануйяна называются “модулярными функциями”. Они предоставили основные принципы, которым следуют все физики, математически исследуя и определяя более высокие измерения. Хотя математики не могут реально видеть более высокие плотности или “измерения”, для определения их свойств они прибегают к аналогии. Классический пример – визуализация аналогии с Плосковиками (Flatlanders) – расой существ, живущей в “плоском” двумерном мире и позже обретшей сферический проход через свой план, сверху донизу. На их уровне восприятия, они могли видеть только круг, сначала маленький, затем достигающий определенной ширины, а потом снова уменьшающийся. Каждый раз, проходя через свой план, они могли видеть только один “слой” сферы. И все же, обладая этой информацией, они смогли математически вычислить свойства сферы и выявить ее существование, хотя она пребывала вне границ их нынешней полосы восприятия. В данном случае, сферу можно рассматривать как “топологию более высокого измерения”. Слово “топология” – разумно звучащий способ передать слово “форма”.
В случае Рамануйяна, модулярные функции определяются как математические операции, которым присуща невероятная и почти неслыханная степень симметрии, позволяющая существование геометрий более высоких плотностей. И внутри этой симметрии, многими и многими разными и синхронными способами, модулярные функции Рамануйяна всегда возвращают нас к числу “восемь” как ключевой организующей силе, стоящей за структурой измерений или плотностей в этой Вселенной. Все это можно видеть в отрывках из книги "Гиперпространство" Мичио Каку. Следует иметь в виду, что теория суперструн очень напоминает эфирные концепции тем, что вся квантовая сфера рассматривается как продукт энергетических вибрирующих “струн”:
“Шриниваса Рамануйян – самый странный человек во всей математике, а возможно и во всей истории науки. Его сравнивали со взрывом сверхновой, освещавшем самые темные и самые важные углы математики вплоть до его трагической гибели от туберкулеза в возрасте 33 лет, как и Римана до него.Работая в полной изоляции от главных течений в своей области, он смог заново вывести то, на что западным математикам потребовалось сто лет. Трагедия жизни Рамануйяна в том, что большинство его трудов было утеряно, а уравнения заново открывались известными математиками. Рассеянные в тетрадях мало понятные уравнения –модулярные функции – самые странные из всех когда-либо обнаруженных уравнений…
Итак, когда центральный икосаэдр расширяется в октаэдр, он совершает небольшой угловой наклон. При этом из определенных его граней "вырастает" тетраэдр. Это смоделировано схемой Роберта Конроя.
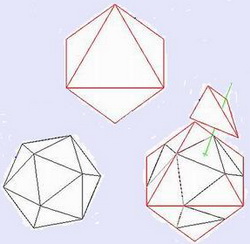
Расширение октаэдра в тетраэдр включает наклон в 45°.
Изначально поле октаэдра совершенно размещается в центре поля тетраэдра. Каждая грань октаэдра, имеющая форму равностороннего треугольника (все внутренние углы по 60° и все стороны одинаковой длины), становится одной трехгранной вершиной звездного тетраэдра. Чтобы оживить это приращение, можно представить, что октаэдр вдруг расцветает как цветок; пока тетраэдры занимают каждый свое место, грани вдруг растут вверх.
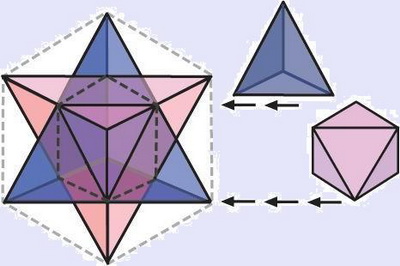
Расширение тетраэдра в куб включает еще один наклон в 45°.
Куб образовывается простым соединением точек на вершинах звездного тетраэдра.

Превращение куба в додекаэдр происходит посредством “плоской крыши”, воздвигаемой на каждой грани куба. Чтобы сформировать пятиугольные грани додекаэдра, двух и трехсторонние области “плоских крыш” сходятся.
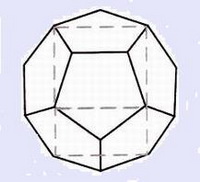
Додекаэдр естественно расширяется в икосаэдр без наклона.
Если вы поставите точку в центре каждого пятиугольника додекаэдра и соедините все полученные точки, то будете иметь набор линий, образующих пятиугольную звезду, создающую форму икосаэдра.

На ниже приведенной фотографии видно, как одна из граней додекаэдра выросла в будущий икосаэдр. На третьем фото показан завершенный икосаэдр (грань в три сферы).


додекаэдр с гранью икосаэдра
Превращение икосаэдра в сферу – самое загадочное преобразование, сводящее воедино всю прямолинейную геометрию. Добавте немного воображения.

 
икосаэдр в сферу
Показанная сфера имеет некоторые изъяны сферичности - просто для идеальной сферы необходимо несколько больше шариков, что естественно при расшинении, но которых не оказалось в наличии. Необессутьте.
Теперь давайте попробуем понять, почему древние рассматривали прямые и изогнутые линии как две противоположности во Вселенной, хотя на самом деле они являются единой вибрацией. Мы чувствуем, что согласно одному образу мышления, прямые линии и геометрии могут представлять собой пространство, а изогнутые линии и спирали - время. Но сейчас мы будем выражать это в более знакомых терминах и скажем, что прямые линии создают форму, а изогнутые – движение и рост этой формы. Иными словами, прямые линии формируют геометрические структуры самих вибраций, а изогнутые - пути для расширения и сжатия этих структурированных частот. Хотя обычно мы не думаем об изогнутой геометрии в связи со звуком и светом, мы знаем, что именно спирали управляют движением между одной нотой октавы и следующей более высокой нотой, или между одним цветом спектра и следующим более высоким цветом.
Попробуем выразить все вышесказанное в более духовном контексте. Во многих древних мистических традициях прямая линия считалась мужской силой и ассоциировалась с Солнцем, а изогнутая – женской силой и ассоциировалась с Луной. Мужские/женские энергии очень легко и интуитивно работают в наших умах. В состоянии покоя клетка спермы образует прямую линию, а яйцеклетка обладает круглой структурой. Тела мужчин по своему строению более тяжелые или прямолинейные, в то время как тела женщин - более плавные и округлые. Тенденция мужского ума – думать более линейно, жестко, посредством математических паттернов “левого полушария”, ум женщин более изогнутый, текучий, с эмоциональными паттернами “правого полушария”. Первобытные мужчины охотились и строили при свете Солнца, используя прямые копья и стрелы для добычи пищи, или позднее прямые доски, молотки и гвозди для строительства сооружений. Женщины готовили еду в плавных, круглых керамических или деревянных горшках, кормили детей плавной, округлой грудью в уединенной темноте пещеры, укрываясь от дневного света, под которым когда-то бродили хищники и злодеи. Кроме того, женщины напрямую связаны с Луной так, как никогда не были связаны мужчины, - своим месячным циклом, демонстрируя еще один уровень, почему древние связывали женский дух с нашим Полуночным Солнцем.
МАГНИТНЫЕ НЕОДИМОВЫЕ СФЕРЫ
Можно и самим попытаться построить некое подобие платоновых тел, используя магнитные неодимовые сферы (неокуб). Более того, вы сможете убедиться, что строиться могут только определенные геометрические формы и из четко определенного количества сфер. Имеет значение и последовательность сборки. В противном случае они будут неустойчивы или вообще не будут собираться в такую структуру. Конечно не стоит забывать, что в данном построении участвуют только электромагнитные силы. Чтобы подключить и силы гравитации, нам придется слетать в космос или туда, где есть невесомость.
  
  
  
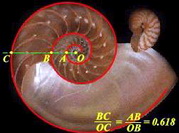
На этих фотографиях можно увидеть и гармоничный рост Платоновых фигур посредством спирали фи. По существу, каждое новое число спирали фи – это сумма двух предыдущих. Самое главное и самое важное из всех сакральных учений о спиралях известно как “Золотое Сечение”.

 МНОГОМЕРНОСТЬ ВСЕЛЕННОЙ
МНОГОМЕРНОСТЬ ВСЕЛЕННОЙ
Cама концепция связи Платоновых геометрий с более высокими планами возникает потому, что ученые знают: там должна быть геометрия; они обнаружили это в уравнениях. Чтобы обеспечить “большее пространство” для появления невидимых дополнительных осей в “скрытых” 90° поворотах, требуется наличие Платоновых геометрий. В способе анализа данных, каждая грань геометрической формы представляет собой разную ось или план, в котором она могла бы вращаться. Когда мы начинаем рассматривать работы Фуллера и Дженни, мы видим, что идея других планов, существующих в “скрытых” 90° поворотах, - просто некорректное объяснение, основанное на отсутствии знания о “сакральных” связях между геометрией и вибрацией.
Весьма похоже на то, что традиционные ученые так и не поймут, что древние культуры могли иметь “упущенную связь”, существенно упрощающую и объединяющую все современные теории физики пространства. Хотя может показаться невероятным, что у “примитивной” культуры имелся доступ к такому виду информации, доказательство налицо. Почитайте классическую книгу Прасада, ибо сейчас можно видеть, что ведической космологии присуще научное мастерство.
Думаете что вы видите? - это взрывающаяся звезда с выбрасывающейся из нее пылью… Но здесь явно имеется и некий вид энергетического поля, структурирующего пыль по мере ее расширения в очень точный геометрический паттерн:


Проблема в том, что типичные магнитные поля в традиционных физических моделях просто не позволяют такую геометрическую точность. Ученые действительно не знают, как понимать такие вещи!
Нижеприведенное изображение – это НОВАЯ туманность, являющаяся совершенным “квадратом”. Однако это все еще двумерное мышление. Что такое квадрат в трех измерениях?
Конечно, куб!
Наблюдаемая в инфракрасном диапазоне туманность напоминает гигантскую сияющую коробку в небе с ярким белым внутренним ядром. Умирающая звезда MWC 922 находится в центре системы и извергает в пространство внутренности из противоположных полюсов. После того, как MWC 922 испустит в пространство большую часть материала, она будет сжиматься в плотное звездное тело, известное как белый карлик, спрятанный в облаках своих остатков.

Хотя отдаленно возможно, что взрыв звезды распространяется лишь в одном направлении, создавая больше пирамидальную форму, то, что вы видите, - это совершенный куб, находящийся в пространстве.
Поскольку все четыре стороны куба имеют одинаковую длину и совершенные 90° углы друг с другом, и вновь, куб обладает структурированными “ступеньками”, которые мы видели на предыдущем изображении, ученые полностью сбиты с толку. Куб обладает еще БОЛЬШЕЙ СИММЕТРИЕЙ, чем “прямоугольная” туманность!
Такие паттерны появляются не только в безбрежности пространства. Они возникают и на самом крошечном уровне атомов и молекул, например, в кубической структуре обычной поваренной соли или хлористого натрия. Ан Панг Цая (Япония) сфотографировал квазикристаллы сплава алюминий-медь-железо в форме додекаэдра и сплава алюминий-никель-кобальт в форме декагональной (десятисторонней) призмы (см.фото). Проблема в том, что вы не можете создать такие кристаллы, пользуясь единичными связанными вместе атомами.

Другой пример – конденсат Бозе-Эйнштейна. Кратко говоря, конденсат Бозе-Эйнштейна – это большая группа атомов, ведущая себя как отдельная “частица”, в которой каждый составляющий ее атом одновременно занимает все пространство и все время во всей структуре. Измерено, что все атомы вибрируют на одной и той же частоте, движутся с одинаковой скоростью и расположены в одной и той же области пространства. Парадоксально, но разные части системы действуют как единое целое, теряя все признаки индивидуальности. Именно такое свойство требуется для “сверхпроводника”. Обычно конденсат Бозе-Эйнштейна может формироваться при крайне низких температурах. Однако именно такие процессы мы наблюдаем в микрокластерах и квазикристаллах, лишенных индивидуальной атомной идентичности.
Еще один подобный процесс – действие света лазера, известного как “когерентный” свет. В пространстве и времени весь лазерный луч ведет себя как единичный “фотон”, то есть, в лазерном луче невозможно выделение индивидуальных фотонов.
Более того, в конце 1960-х годов английский физик Герберт Фрёлих предположил, что живые системы часто ведут себя как конденсаты Бозе-Эйнштейна, только в крупном масштабе.
 
Фотографии туманности предлагают ошеломляющее видимое доказательство того, что геометрия играет большую роль в силах Вселенной, чем может поверить большинство людей. Наши ученые могут лишь сражаться за понимание этого феномена в рамках существующих традиционных моделей.

|

